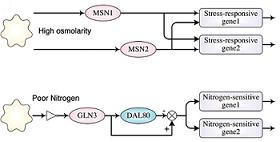
Network motifs have been identified in a wide range of networks across many
scientific disciplinesand and are suggested to be the basic building blocks of
most complex networks. Nonetheless, many networks come with intrinsic and/or
experimental uncertainties and should be treated as stochastic networks. The
building blocks in these networks thus may also have stochastic properties.
We studied stochastic network motifs derived from families of mutually
similar but not necessarily identical patterns of interconnections,
established a finite mixture model for stochastic networks, and developed an
expectation-maximization algorithm for identifying stochastic network
motifs.
— Rui Jiang, et al., Network motif identification in stochastic networks.
Proc. Natl. Acad. Sci. USA, 103.
A common property of many large networks such as the World Wide Web and
biological interaction networks is that the vertex connectivities follow
a scale-free power-law distribution. This feature was found to be a
consequence of two generic mechanisms: (i) networks expand continuously
by the addition of new vertices, and (ii) new vertices attach
preferentially to sites that are already well connected.
— Barabasi, et al., Emergence of scaling in random networks. Science,
286.
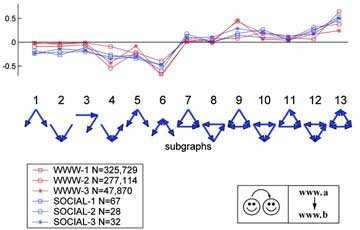
Complex networks are studied across many fields of science. Network motifs,
patterns of interconnections occurring in complex networks at numbers that
are significantly higher than those in randomized networks, have been
discovered in networks from the World Wide Web to social networks and
aresuggested to perform information processing, even though they describe
very different elements in different networks. Motifs may thus define
universal classes of networks and help us to uncover the basic building
blocks of most networks.
— Alon, et al., Network motifs: simple building blocks of complex networks.
Science, 300.